파랑특성 및 관측방법 (I)
- 조회 : 13286
- 등록일 : 2017-12-04
『파랑특성 및 관측방법 (I)
운용해양예보연구센터 임학수 책임연구원
1. 서론
지구온난화에 따른 해수면 상승, 태풍의 빈도 변화와 강도 증가, 기압경사에 의한 강한 돌풍에 따른 너울성 파랑 등 자연적인 원인에 의한 동해안 연안침식이 점차 가중되고 있다.
해양수산부에서 발표한 2016년도 해안별 연안침식 실태조사 결과에 따르면 동해안 82개소 모니터링 해안 중 42개소와 30개소가 각각 우려와 심각 등급을 받았다. 동해안에서 심각하게 발생하고 있는 연안침식의 주요원인은 자연적 원인과 인위적 원인으로 구분할 수 있다.
특히, 자연적 원인 중 가장 큰 원인은 너울성 고파랑에 의한 해안선 방향의 해빈류(longshore current)와 외해 방향으로 빠져나가는 외해류(cross-shore current) 또는 이안류(rip-current)에 따른 해빈침식과 외해로 유출되는 토사이동으로 규명되고 있다.
외해류와 이안류는 주로 태풍 또는 기압경사에 의해 먼바다에서 발달한 너울이 연안으로 해안선과 직각 방향으로 전파되면서 낮은 수심에서 천수변형(shoaling)과 쇄파(wave breaking)되면서 생성되는 파랑류(wave-induced current)의 형태이다. 본 글에서는 연안으로 전파되는 파랑의 특성을 살펴보고 실해역에서 파랑 관측 및 분석에 대해 주로 다루고자 한다.
2. 파랑특성
파랑은 바다에서 바람이 해수면 위를 지속적으로 불 때 생기는 풍파와 먼 바다에서 발생한 풍파가 연안으로 전파되는 너울을 모두 파랑이라고 한다. 풍파는 파봉(wave crest)이 가파른 마루를 가지고 있으며, 파곡(wave trough)이 둥근 모양의 골을 가지고 있고, 파장과 주기가 비교적 짧다. 너울은 마루가 둥글고, 파장이 길다.
파랑은 우선 파고(wave height), 파장(wave length), 주기(wave period)로 특성을 구분할 수 있다. 파고는 파곡에서 파봉에 이르는 연직거리이다. 파장은 파봉에서 파봉 또는 파곡에서 파곡에 이르는 거리이다. 주기는 파봉에서 파봉 또는 파곡에서 파곡이 연속해서 한 지점을 통과하는 시간이다. 파속(wave celerity 또는 speed) 은 파장을 주기로 나눈 속도를 나타낸다.
또한, 파랑은 바람에 의해 전달되는 에너지를 효과적으로 운반한다. 파랑은 개별 파랑이 아닌 군파 형식으로 에너지를 전파하며 파랑의 단위면적 당 에너지(wave energy)는 파고의 제곱에 비례한다. 파랑이 이 에너지를 전달하는 에너지 양(energy flux)은 파랑에너지를 주기로 나눈 값이며, 파속 또는 군속도(group velocity)에 비례한다. 군속도는 여러 성분파의 합성파(wave envelope)가 진행하는 파의 속도를 의미한다.
즉, 일정거리에서 파가 도달하는 시간을 구하기 위해서는 거리를 파속으로 나누는 것이 아니라 군속도로 나누어야 한다. 군속도는 심해파에서 파속의 1/2이며, 천해에서는 파속으로 대체할 수 있다.
수심이 낮은 천해에서 발생하는 외중력파(infragravity wave)는 파의 전파과정 중 비선형성에 의해 형성된 장주기 군파(group wave)가 쇄파에 의해 구속이 이완되면서 해안선 가까이에서 처오름, 월파, 연안침식을 유발한다. 외중력파는 안목해안에서 관측한 파랑자료를 분석한 연구에서 자세히 소개할 예정이다.
2.1 선형파의 이차원 변형
일반적으로 파동이론에서 수심은 고정된다. 그러나, 이차원 파랑의 진행방향으로 수심이 변하면 파고가 변하게 된다.
해안선으로 접근하면 수심이 작아지면서 파고가 증가하는 천수변형(shoaling)이 발생하며 결국에는 쇄파(wave breaking)에 이르게 된다.
이차원 파랑변형은 이와 같은 천수변형과 쇄파를 의미하며 또한, 지형 또는 장애물에 의한 파 반사(reflection), 지형 또는 장애물에서의 처오름(runup)과 월파(overtopping) 및 투과(transmission), 바닥에서의 마찰에 의한 에너지 감쇠(energy dissipation) 등이 포함된다.
천수변형 및 쇄파
천수변형은 파랑이 수심이 낮은 천해로 접어들면서 발생한다.
천해에서는 파속과 파장이 감소하므로 단위면적당 파랑에너지가 증가하고 파고도 높아진다.
천수변형 중 주기는 변하지 않는다. 파의 마루가 너무 가파르면 불안정해지고, 파는 앞으로 감기고 쇄파된다. 이런 천수변형은 파고가 천해 수심과 거의 같은 크기가 될 때 발생한다.
쇄파는 파장에 대한 파고의 비인 파형경사(wave steepness)와 해안경사(beach slope)에 따라서 붕파(surging wave), 권파(plunging wave), 붕괴파(spilling wave)로 구분할 수 있다.
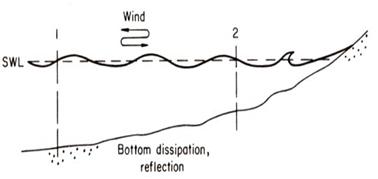
그림 1. 파의 천수변형과 쇄파
반사
파랑의 반사는 자연지형(자연해빈, 해안절벽 등)과 인공지형(방파제, 호안 등)에서 발생하며 입사파고 에너지의 일부가 외해로 반송됨을 의미한다. 입사파고 대비 반사파고의 비를 반사율이라고 한다.
반사율은 지형 또는 구조물의 경사 또는 표면 거칠기(roughness) 및 공극률 등에 따라 달라진다.
일반적으로 경사도가 클수록 그리고 입사파의 파형경사가 작을 수로 파 반사가 크게 발생하며 완전 중복파에 접근하게 된다. 파장에 비하여 파고가 아주 작은 파가 경사도가 직각인 직립벽면에 부딪히면 완전반사가 발생하여 중복파가 발생하게 된다.
이 경우에 표면이 아주 매끄러워 마찰손실이 없으면 반사율은 1에 가깝다.
이와는 반대로 파형경사가 크고 바닥경사도가 작을 때는 많은 쇄파가 발생하여 에너지가 손실되므로 파 반사가 적게 되며 부분 중복파를 형성하게 된다.
처오름
처오름은 경사면을 따라 파가 거슬러 올라가는 최고점과 정수면 사이의 연직거리를 의미한다.
일반적으로 처오름은 해안경사와 심해파 파형경사에 의존하여 산정한다.
처오름 역시 경사면의 기울기와 거칠기에 의존하며 각 표면의 조도에 대한 계수를 이용하여 계산한다.
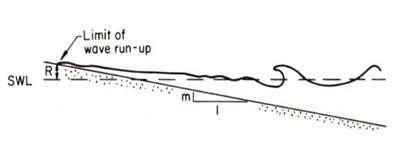
그림 2. 파의 처오름
월파 및 투과율
구조물의 마루높이가 처오름 보다도 작을 경우 월파가 발생한다.
이 월파는 구조물의 이면에 낙하하여 파랑을 발생시킨다. 입사파고에 대한 통과파고의 비를 투과율이라 한다.
2.2 삼차원 파랑전파
삼차원 파랑전파는 전파과정 중 수심 변화에 의하여 파향과 파고가 변하는 굴절(refraction)과 해안선 또는 도서 등 측면 경계에 의하여 파향과 파고가 변화는 회절(diffraction)로 나뉘어진다.
실제 해역에서는 회절과 굴절이 동시에 발생한다.
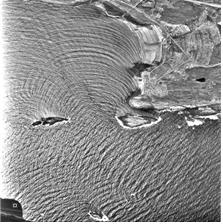
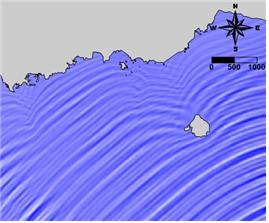
그림 3. 실해역에서 파의 굴절과 회절: (좌) 항공사진, (우) 수치모델
굴절
굴절은 수심이 변하기 때문에 파가 휘어지는 현상이다. 얕은 물속의 파는 깊은 물속의 파보다 느리게 움직이므로 수심에 따라 파봉선(wave crest line)이 변하며 파가 휘어진다.
파가 해안선에 비스듬하게 접근하는 경우 해안에 가까운 파는 얕은 물에 있어 해안에서 멀리 떨어진 깊은 물에 있는 파보다 느리게 움직인다. 이 경우 더 깊은 물 속에서 파봉선이 빠르게 접근하여 해안과 평행하게 되는 경향이 나타난다.
굴절은 섬 주변에서도 발생한다.
한 방향에서 접근하는 파가 섬 주위를 감싸면 파의 파봉선은 섬의 모든 면에서 평행하게 접근한다.
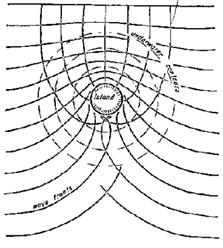
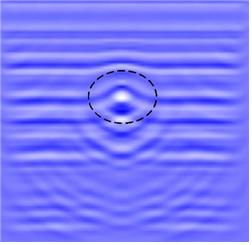
그림 4. 섬으로 접근하는 파의 굴절: (좌) 개념도(Dean and Dalrymple 1991), (우) 수치모델
회절
회절은 파가 방파제 또는 돌출된 섬과 같이 장애물을 만날 때 주로 발생한다. 방파제나 섬을 지나친 파는 음영 지역(shadow zone)으로 파향선(wave ray)이 바뀌고 파랑 에너지를 전파시킨다.
파가 회절되면서 수심의 변화에 따라 굴절도 함께 발생한다.
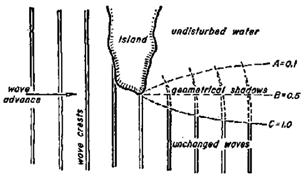
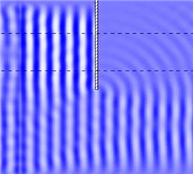
그림 5. 돌출된 섬으로 접근하는 파의 회절: (좌) 개념도(Dean and Dalrymple 1991), (우) 수치모델
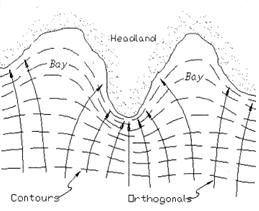
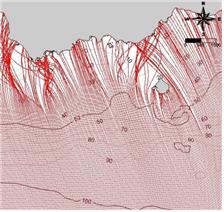
그림 6. 해안으로 접근하는 파봉선과 파향선: (좌) 개념도(Dean and Dalrymple 1991), (우) 수치모델
-다음편에 계속-
References and Recommended Readings:
1. Dean, R.G. and Dalrymple R.A., 1991. Water wave mechanics for engineers and scientist. World Scientific, Singapore.
2. Nielsen, P., 1992. Coastal bottom boundary layers and sediment transport. World Scientific, Singapore, 324p.
3. Nielsen, P., 2009. Coastal and estuarine processes. World Scientific, Singapore, 343p.V., McLean, S., Doscher,
 온라인 역사관
온라인 역사관